解析几何 点线面常见的关系

平面方程

http://www.math.sjtu.edu.cn/upload/teachers/11104/%E7%AC%AC07%E7%AB%A0%E5%90%91%E9%87%8F%E4%BB%A3%E6%95%B0%E4%B8%8E%E7%A9%BA%E9%97%B4%E8%A7%A3%E5%87%A02.pdf

一般式

Ax +By +Cz + D = 0

其中n = (A, B, C)是平面的法向量，D是将平面平移到坐标原点所需距离（所以D=0时，平面过原点）

点法式

由方向和一个点确定一个平面

平面的点法式方程

已知平面上任意一点M0(x0, y0, z0) 和法线向量A B C

那么其平面方程为

A(x-x0) + B(y-y0)+ C(z-z0) = 0

image

直线方程

直线方程的各种形式 https://zhuanlan.zhihu.com/p/26263309

点法式 (由方向和一个点确定一条直线)

A(x-x0) + B(y-y0) = 0

三维空间中的直线一般方程

空间中的直线可以看作是两个平面的交线

image

空间中的直线参数式方程

image

PS 光线追踪中的直线的定义, 就是使用的向量式方程

空间中直线的标准方程

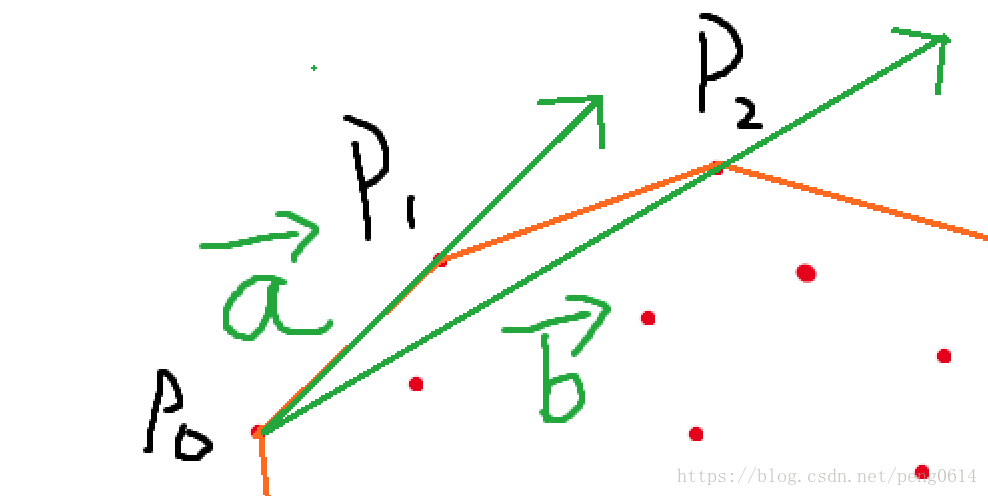
image

求向量A 在 向量 B 上的投影长度

利用点乘 a.b = A   B cosθ
其中 A cosθ 就是投影的长度

一个重要的变形

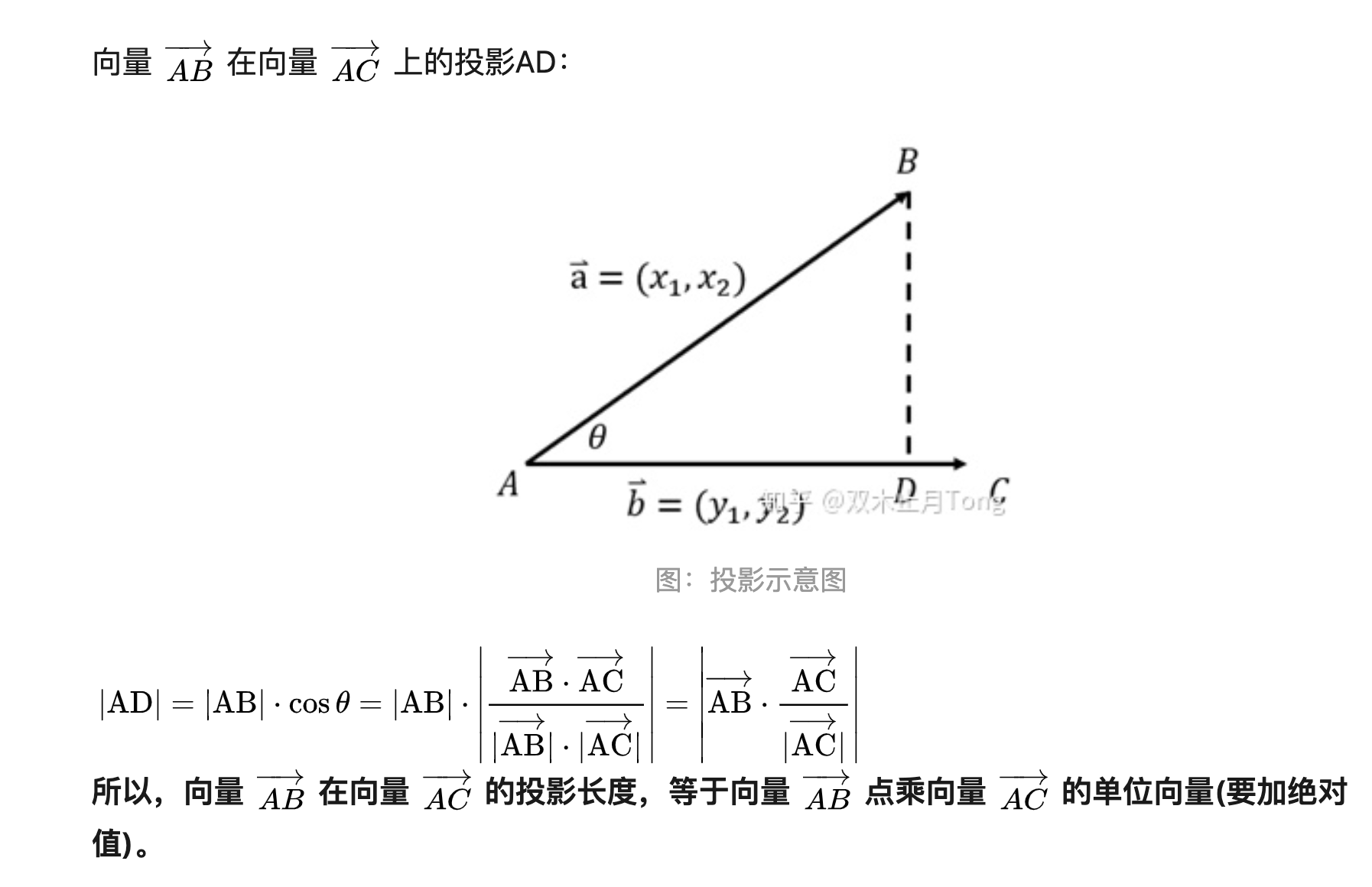
image

求点到直线的最短距离

需要用到上面的结论

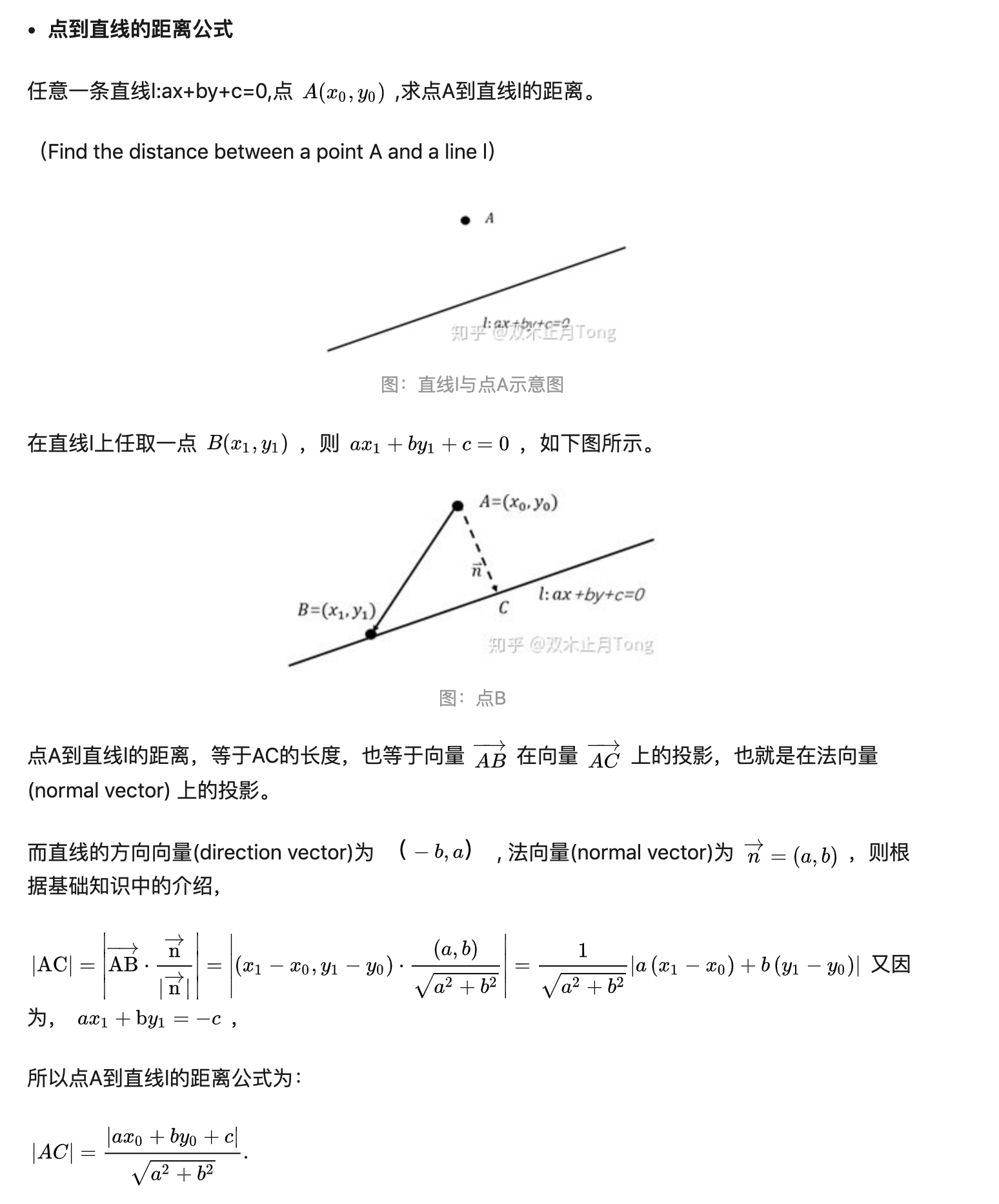
image

判断点到面的最短距离

点到直线最短距离的延伸

点到平面的距离公式 - 翰墨小生 - 博客园

image

判断点是否在矩形内

就是看点的 x y 是否在矩形的 x y 中

bool IsPointInRect(const Rect& rc, const Point& p) 
{
    double xr = (p.x - rc.p1.x) * (p.x - rc.p2.x);
    double yr = (p.y - rc.p1.y) * (p.y - rc.p2.y); 
    return ( (xr <= 0.0) && (yr <= 0.0) ); 
}

延伸: 判断点是否在三维巨星盒子内

上面已经考虑了 xy 的情况。 再考虑 xz 的情况就好。并不用考虑yz

判断点是否在圆内

原理就是计算点到圆心的距离d，然后与圆半径r进行比较

PS. 另外没有必要开平方

double PointDistance(const Point& p1, const Point& p2)
{
  return std::sqrt( (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y) );
 
}

对于球也是同样道理

判断两个矩形是否相交

bool IsRectIntersect(const Rect& rc1, const Rect& rc2)
 
  {
      return ( (std::max(rc1.p1.x, rc1.p2.x) >= std::min(rc2.p1.x, rc2.p2.x))
              && (std::max(rc2.p1.x, rc2.p2.x) >= std::min(rc1.p1.x, rc1.p2.x)) 
              && (std::max(rc1.p1.y, rc1.p2.y) >= std::min(rc2.p1.y, rc2.p2.y))
              && (std::max(rc2.p1.y, rc2.p2.y) >= std::min(rc1.p1.y, rc1.p2.y)));
   
   }

判断点是否在线段上

计算几何—判断点是否在线段上_LzyRapX-CSDN博客_判断点是否在线段上

先判断点是否在这个线段构成的矩形区域内 (矩形的对角线就是这个线段)

这样就排除了点在线段的延长线可能

第一步 简单点说就是点的x y 都小于线段两个端点的 x 和 y

之后再看点P和任意一个端点构成的线是否和线段斜率相等 (也即是两个向量的方向是否一致)

也就是再利用叉积的性质: 平行OR 方向完全相反的向量的叉积的标量值是0

(也可以说是几何意义: 两个向量构成的平行四边形的面积)

bool onSegment(point Pi , point Pj , point Q)
{
    if((Q.x - Pi.x) * (Pj.y - Pi.y) == (Pj.x - Pi.x) * (Q.y - Pi.y)  //叉乘 
       //保证Q点坐标在pi,pj之间 
       && min(Pi.x , Pj.x) <= Q.x && Q.x <= max(Pi.x , Pj.x)    
       && min(Pi.y , Pj.y) <= Q.y && Q.y <= max(Pi.y , Pj.y))
        return true;
    else
        return false;
}

判断点在直线的左右哪一侧

题目1判断两个点是否在直线的同一侧

已知P(0,0), Q(3,2)两点，试判断P,Q是否在直线2x+3y=4的同一侧。

解：直线2x+3y=4即 直线2x+3y-4=0
把P、Q代入2x+3y-4
得到
2*0+3*0-4=-4 < 0
2*3+3*2-4=8 > 0
所以在两侧！

题目2

PS 某一点在直线左右侧左右方向是相对前进方向的

叉积的一个非常重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系：

若 P × Q > 0 , 则P在Q的顺时针方向。

若 P × Q < 0 , 则P在Q的逆时针方向。

若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。

判断两条线段是否相交

前端图形学的数学基础 · 语雀

向量法

对于任意两条线段, 另一个线段的两个断点在笨线段的两边

image

判断线段和圆的关系

关系: 相交 相切 包含 没有关系

如何判断一条线段和一个矩形或者圆相交？ - 知乎

image

这里 x-c 表示线段上任意一点x 和 圆心 c 的构成的向量

x-c ^2 = r^2. 可以理解为一种推导出来的关系。 我不理解为什么用这个作为圆的方程

根据上面的求出的来的 t 表示在这个直线方向上, 要想和圆有交点, t 应该满足的大小

如果给出的 t < 求出来的t。那么就是在圆内

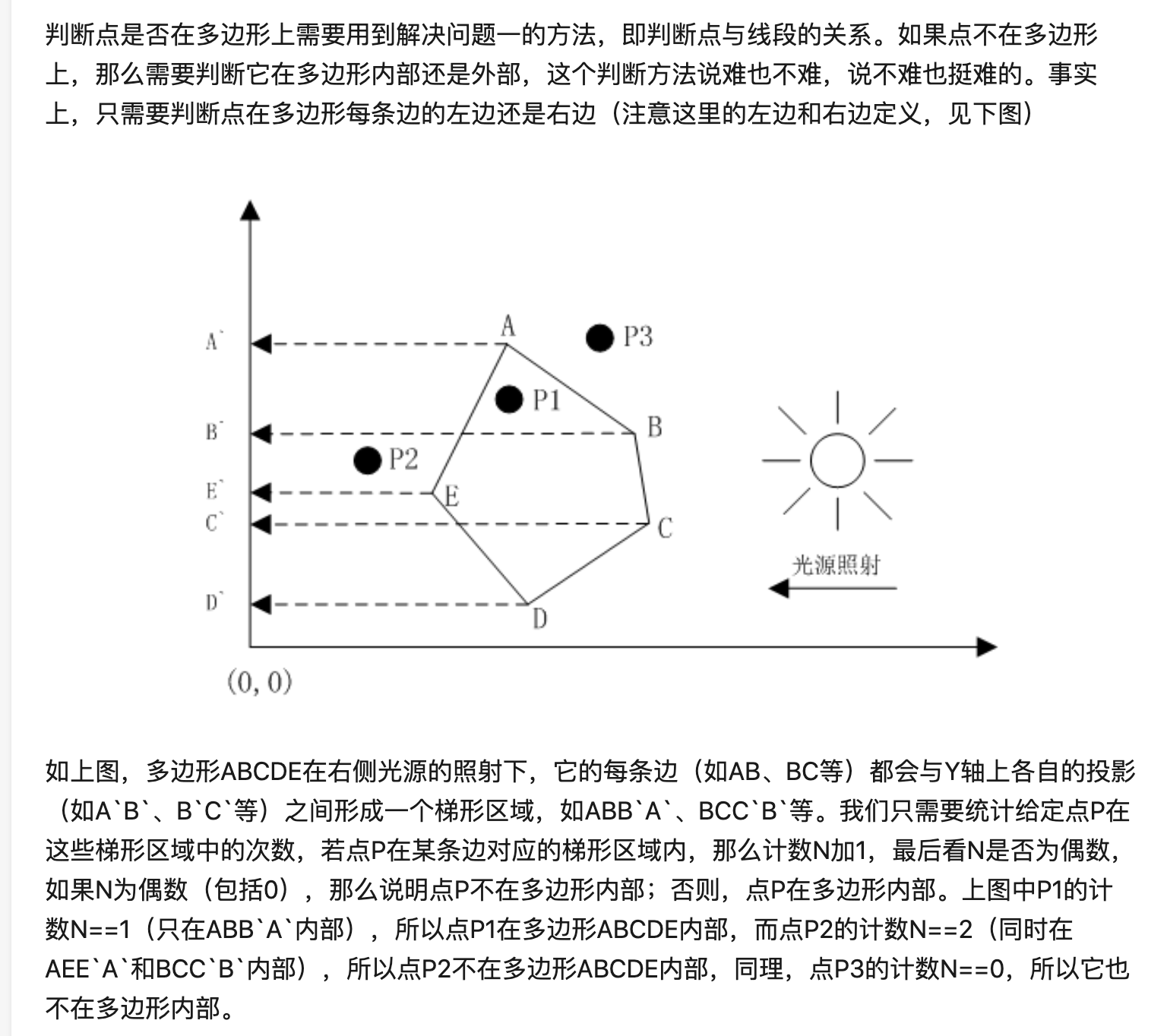
判断点是否在多边形内

图形学常见的点、线、面位置关系判断算法及其代码实现_smilejiasmile的博客-CSDN博客_图形学常见的点、线、面位置关系判断算法

最常用的方法是射线法。以P点为起点，向左方做射线L，然后沿着L从无穷远处开始向P点移动，当遇到多边形的某一条边时，记为与多边形的第一个交点，表示进入多边形内部，继续移动，当遇到另一个交点时，表示离开多边形内部。

由此可知，当L与多边形的交点个数是偶数时，表示P点在多边形外，当L与多边形交点个数是奇数时，表示P点在多边形内部。

判断点和多边形的关系

(点是否在多边形内的另一种判断方式)

关系: 没关系(在多边形外) 在多边形上。在多边形内

如何判断一条线段和一个矩形或者圆相交？ - 知乎。周智的回答

image

判断线段和多边形的关系

关系: 没关系 相交 包含 如何判断一条线段和一个矩形或者圆相交？ - 知乎。周智的回答

判断线段与多边形的各条边是否相交，若是，则线段与多边形属于“相交”关系；

如果线段与多边形的任何边都不相交，那么我们接着判断线段的任意一个端点是否在多边形内部，

若是，则整条线段肯定在多边形内（即“包含”关系）；

若不是，则整条线段肯定都在多边形外部（即“无关联”关系）。

求点在平面上的投影

计算点在平面上的投影坐标 - NobodyZhou - 博客园

求直线在平面上的投影

判断点到面的最短距离的延伸

重心坐标

重心坐标 - 维基百科，自由的百科全书

在 三角形 情形中，

重心坐标也叫面积坐标，因为P点关于三角形ABC的重心坐标和三角形PBC, PCA及PAB的（有向）面积成比例。

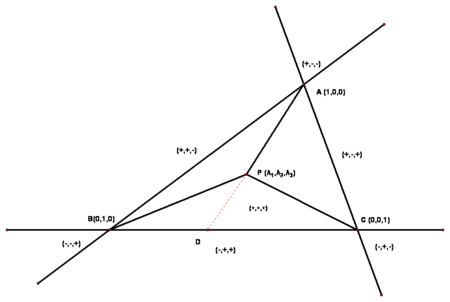
image

PBC, PCA及PAB 面积比是 λ1 λ2 λ3

且 λ1+λ2+λ3 = 1

PBC 是 A点 对面的三角形

P = λ1A + λ2B + λ3C

延伸

计算几何第一周：凸包（Convex Hull） - 知乎

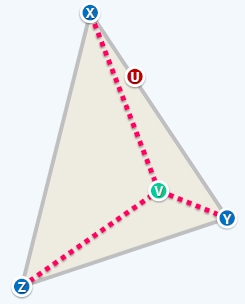
凸性(Convexity)

以颜色为例

假设x,y,z是三种颜色，如果仅以x,y就能调出来的颜色，那么如u所示它一定会落在x,y这条线上；(利用刚才上面说到的面积, 使用求极限的思想就可以推断出)

若需要x,y,z三种 一起，那么如v所示会落在以x,y,z三点连成的三角形内部。

image

凸包

给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，使得它能包含点集中所有的点.

凸包最常见的应用是求平面上距离最远的两个点。

在凸包上找两个连续的点，如果下一个点是凸包上的点，则b在向量a的右端。 image